An Application of Topology to Gimbal Locking

I recently learned of a fun “application” of topology though this has been widely known for decades, probably. I’ll present it from my own perspective. A gimbal is a tool built from three nested rings, meant to model rotations in $\mathbb{R}^3$ and also used by older systems for navigation and orientation. Let $SO(3)$ denote the Lie group of $3\times 3$ real matrices with $\det = +1$; these give rotations on $\mathbb{R}^3$ and together, they form a space which one can identify as being diffeomorphic to $\mathbb{RP}^3$, real projective space; I’ll describe why later.

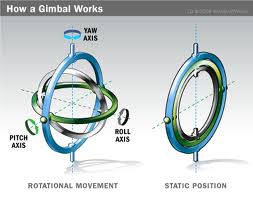
However, we see that there’s an issue with the gimbal as a model for rotations. We have 3 degrees of freedom most of the time but if all three rings lie in the same plane, then they cannot rotate on the axis perpendicular to that plane; so you lose a degree of freedom. This is called gimbal locking. Now, I’m not sure if this is historically accurate or just was in the movie but supposedly, in the Apollo 13 space mission, their spacecraft became unstable because their navigation computer (specifically the inertial measurement unit) got into a gimbal lock. That wasn’t their biggest problem but was one of them.

Anyways, another way to know that gimbal locking must happen is that the three rings rotating can be modeled by the 3-torus $T^3$ (just three copies of a circle, each circle representing the angle of rotation of one of the rings). In fact, we can see that any model based on using three angles will also fail, even if we made something more elaborate than a gimbal, even if it’s a computer program that tracks the three angles instead of something mechanical. Here’s the topology statement:

Lemma: There does not exist a covering map $T^3 \to SO(3)$; in particular, there can’t be a proper map that is a local diffeomorphism at every point (such maps are always covering maps). This means there is at least some point where the rank of the map is less than 3, a loss of at least one degree of freedom.

Proof: The space $\mathbb{RP}^3 = SO(3)$ is double covered by the 3-sphere $S^3$ and $\pi_4(S^3) = \mathbb{Z}/2$. In fact, it’s generated by the suspension of the Hopf fibration $\eta:S^3 \to S^2$ and becomes stable under suspension starting here. Since covering maps induce isomorphisms on all higher homotopy groups, $\pi_4(SO(3)) = \mathbb{Z}/2$ as well. But $\pi_i(T^3) = 0$ for $i>1$. Hence, any map $T^3 \to SO(3)$ will always fail to be a covering. $\square$

Nonsequitur: The fact that a proper, local diffeomorphism $f:M \to N$ of connected, smooth $n$-manifolds is a covering map is a result that was “affectionately” called the Comps Lemma where I went to grad school. It was a lemma that often was useful on the comprehensive exams.

One way to avoid gimbal locking is then to use maps $S^3 \to SO(3)$ instead of $T^3 \to SO(3)$. A natural map to use is a double cover which we can form in a number of ways because $S^3$ has a number of guises as the following three Lie groups, all isomorphic (as Lie groups) to each other: $SU(2)$ which consists of $2 \times 2$ complex matrices with $\det = +1$, $Sp(1)$ which consists of unit quaternions, and $\text{Spin}(3)$ which is the group of units in the even part of the real Clifford algebra $Cl(3,0)$. This even part, denoted $Cl_0(3,0)$, is isomorphic as an $\mathbb{R}$-algebra to the quaternions $\mathbb{H}$; so it’s clear how the latter two are isomorphic. But also, we may write elements of $SU(2)$ as \(\begin{pmatrix} \alpha & \beta \\ -\bar{\beta} & \bar{\alpha} \end{pmatrix}\)

where $\alpha,\beta \in \mathbb{C}$ and $\bar{\alpha}$ means complex conjugation. The condition on the determinant means $|\alpha|^2 + |\beta|^2=1$. Now, if we write $\mathbb{H} \cong \mathbb{C} \oplus \mathbb{C}j$ where $j^2 = -1$, then it’s more clear how to get an isomorphism $SU(2) \cong Sp(1)$. I’m not sure which presentation NASA favors, but I’ve heard it’s the quaternionic one since that’s amenable to faster computations than doing matrix multiplication. Of course, quaternions and more generally, spinors, play a major role in physics, such as in the Dirac equation. In mathematics (related to the physics), it underlies one of the great triumphs of the 20th century: the Atiyah-Singer Index Theorem.

I’ll end by explaining why $SO(3) \cong \mathbb{RP}^3$. Recall that $\mathbb{RP}^n$ can be obtained by taking a closed ball in $\mathbb{R}^n$ and identifying the antipodal points on the boundary sphere. So take a ball of radius $\pi$ in $\mathbb{R}^3$. Take a point $p$ on the interior. It represents a counterclockwise rotation along the vector $\vec{p}$ (orientation determined also by this vector) by an angle of $|\vec{p}|<\pi$. If $p$ is on the boundary, then we’re rotating by an angle of $\pi$. But this rotation could also be achieved by taking $-\vec{p}$; it amounts to a clockwise rotation along $\vec{p}$ by $\pi$ which is the same as a counterclockwise rotation by $\pi$. Hence, we must identify the antipodal points.

Alternatively, take the standard unit sphere $S^2 \subset \mathbb{R}^3$ (the radius is unimportant). Any axis of rotation will intersect $S^2$ orthogonally and hence, be orthogonal to its tangent plane. Take the unit circle in that tangent plane to describe the angle of rotation. What we get is a circle bundle on $S^2$ built from its tangent bundle (whose Euler class is 2). The total space of this bundle is $\mathbb{RP}^3$.