Center of Mass of $N$ Points in Space

Recently, a friend introduced me to a problem posed by Presh Talwalkar in a video here. The problem is as follows. Take an equilateral triangle and inscribe a circle into it. Pick any point $P$ on the circle and connect line segments from $P$ to each of the vertices. The challenge is to show that the sum of the squares of the lengths is actually a constant, independent of the placement of $P$. The video gives a nice proof of the fact but when one studies it more closely, we see that we can actually generalize the statement quite a bit.

First of all, it turns out that it’s not important that the radius of the circle happens to inscribe the triangle. You can take any radius $R$ for the circle so long as it’s still centered at the middle of triangle. But also, it’s not important that the points be arranged in this equilateral-triangular way. Indeed, so long as the circle is centered at the center of mass of the three points, the statement is still true. And it doesn’t have to be three points; it can be any number of points $N$. Lastly, it doesn’t even have to be in the plane, it can be in any $(k+1)$-dimensional space and you just ask that $P$ be on a $k$-sphere. So to summarize:

Proposition: Consider any collection of $N$ points $Q_1,…,Q_N$ in $\mathbb{R}^{k+1}$ and let $C$ be the center of mass of these points. That is, viewing the points as vectors, $C = \frac{1}{N} \sum^N_{i=1} Q_i$. Take a point $P$ that sits on a $k$-sphere of any radius, centered at $C$. Then the following sum is constant, independent of where $P$ is placed: $\sum^N_{i=1} |P - Q_i|^2$.

My friend made an excellent Desmos widget here which shows the situation in $\mathbb{R}^2$ with $N$ points and any radius circle. There is a slider to change $N$, another for the “spread” of the points, and also one to change the radius $R$. With that all fixed, one can change the location of $P$ on the circle and observe that the sum of the lengths squared, is unchanged.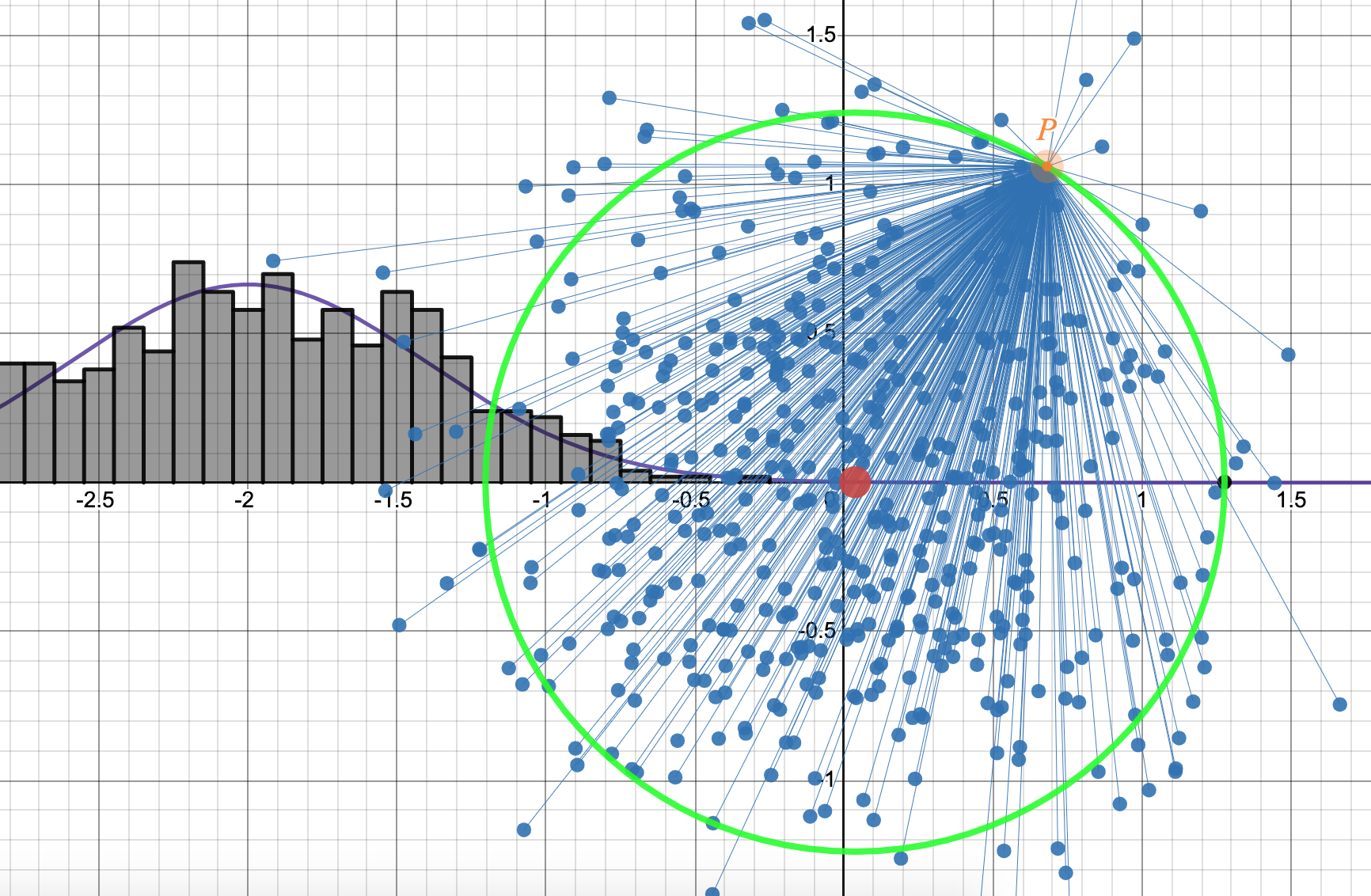

Here is a sketch of a proof of the statement. Without loss of generality, one can assume that the center of mass is at the origin. This is because coordinates aren’t intrinsic to Euclidean space and also, the whole proposition doesn’t change if you translated all the points simultaneously to the origin (or applied any other isometry). Then, to write out the lengths squared, one can use, say, the dot product and you’ll find there are three types of terms. The first are those coming from $|P|^2 = R^2$ and so it doesn’t depend on the location of $P$. Remember, a $k$-sphere centered at 0 with radius $R$ satisfies the equation $x^2_1+…+x^2_{k+1} = R^2$.

There are also terms $|Q_i|^2$ which depend only on the location of the points and not at all dependent on $P$. Lastly, there are the cross terms but when you collect them all together, you’ll find that it amounts to a dot product $P \cdot \sum^N_{i=1} Q_i$. But the sum here is just the center of mass times $N$ and since $C = 0$, then the cross terms vanish.

This proposition is very straightforward to state and also to prove but it’s also a proposition I don’t think I could come up with on my own. It’s maybe only after experimenting a bit with, say, Desmos, that one notices some of these patterns and formulates the proposition. One thing I also like about the proof is because it highlights something I hadn’t appreciated before: Cartesian coordinates give us a lot of extra structure on the topological space underlying $\mathbb{R}^n$, call it $X$. The coordinates give a vector space plus an inner product and therefore, also a norm to measure distance. And if you’re in $\mathbb{R}^3$, you can even define a cross product. But the $N$ points spread out in space is just a geometric notion and one can also define the center of mass without needing vector space structure though it may take a more longwinded definition, maybe borrowing from physics. But Euclid himself could have thought about the problem without resorting to vector spaces or dot products. We need something like a norm to talk about the problem but in fact, only need something weaker: a metric $d:X \times X \to \mathbb{R}_{\geq 0}$. Then, if you want to bring in vector space and dot product structure, you could just declare the center of mass to be the origin; this doesn’t change any of the geometric content but it now gives a way to study geometry via algebra like the dot product.

Here is another proposition that is maybe easy to prove but not so easy to discover (for me). Let’s return to the equilateral triangle example and consider a circle of any radius, centered at the middle of the triangle. Let’s call the lengths of the line segments from the vertices to a point $P$ on the circle to be $a,b,c$. One can form a new triangle using the side lengths $a,b,c$ in the following way. Rotate the equilateral triangle about one of its vertices by $\pi/3$ radians; we’ll rotate the circle, point $P$, and all the line segments as well (my friend said this idea may be in another of Presh Talwalkar’s videos though I’m happy to say I thought of it myself). Then you’ll find a triangle with side lengths $a,b,c$. Here’s a visualization, again thanks to my friend. In the Desmos widget, you can change an angle $\alpha$ which determines $P$ and also the radius of the circle, here labeled $m$. There is also a quantity $A$ which is the area of the triangle. As you move $P$ around, the area stays constant even though this new triangle changes shape!

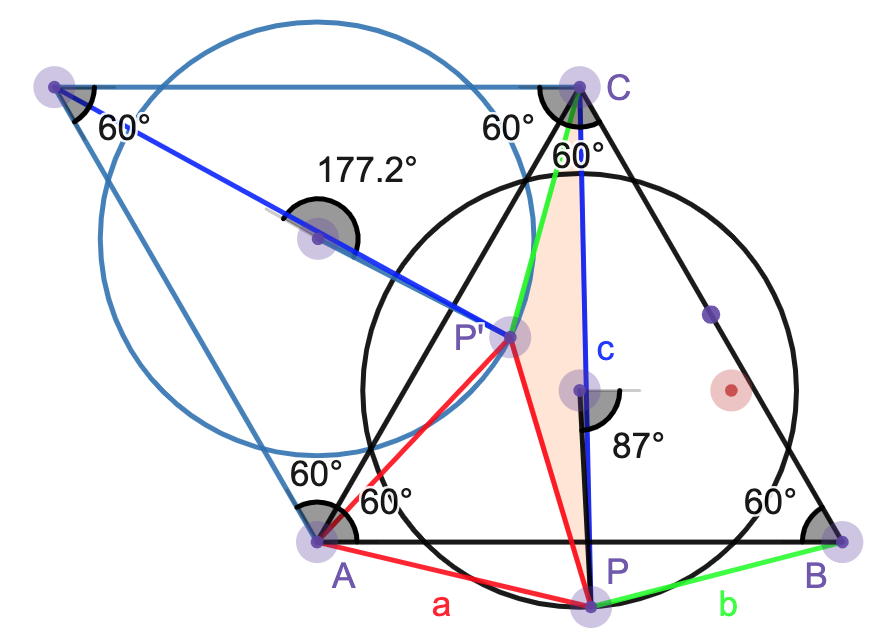
Proving this is a fun exercise. One can use Heron’s formula for the area of triangles; the formula only uses the side lengths $a,b,c$ as input and one version of it involves $a^2+b^2+c^2$ and also $a^4+b^4+c^4$. We know the former is constant and one can show that the latter is also constant using, say, some complex numbers and 3rd roots of 1. Then knowing that those terms are constant plus this version of Heron’s formula gives us the desired result that $A$ is constant even as $P$ moves around. In studying this argument, one could try forming regular $N$-gons instead of just equilateral triangles and then forming some new triangles. There are similar statements to the one above. Certain triangles will have the same area even as $P$ moves around. Other triangles don’t have the same area on their own but the sum of all their areas is constant. There’s a lot to explore since there are lots of different shapes to make and one can ask which ones have constant area, independent of the placement of $P$.